Логические задачи : Дефект масс

	"Логические задачи" - это познавательно-развлекательный проект для непрокисших мозгов. Задачи на логику, нестандартное мышление. Не всегда самое очевидное решение - правильное. Но иногда всё оказывается проще, чем кажется на первый взгляд.
Задачи на логику и сообразительность
Главная \| О проекте \| Все задачи-1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C \| Добавить задачу

О сайте
Гостевая книга
ЧаВо

Пользователи
RSS

Поиск на сайте

запомнить меня

Задачи

Переливания и взвешивания

Теорвер, комбинаторика

Задания на наблюдательность

требуется помощь

Чисто поржать

Детские с подковыркой

Данетки

Текущие:

  Мой любимый грех (с)
  Математика в архитектуре
  Не сыпь мне соль на рану
  «Геометрическая»
  Высказывание Ломоносова
  Наверное, не про яблоки
  Комерция
  Везде градусы
  Вагончик тронется, вагончик тронется..
  Спасибо медикам и католикам))
  Специальная купюра
  Студенческая смекалка
  Эллипс vs Круг
  Современные технологии. Немецкий стандарт.
  Спортивная
  философская
  Про газету
  печатная монета
  Купюра евро
  Древние изобретения
  Биометрические паспорта
  Новый глава
  В далеком созвездии тау Кита... 8)))
  Огородное
  Средневековое строительство
  Жестокое наказание
  Их нравы - 4
  Европейский стандарт

Разгаданные недавно:

  этот модный тандыр
  Из Что-Где-Когда
  Может ли такое быть?
  Что изображено?
  Да на тебе пахать надо!

Справочная

Признаки делимости
Площади фигур

Реклама

Версия для смартфонов

задача: Дефект масс

Задачу прислал: ivana2000

Открытый сосуд объема V, имеющий форму усеченного конуса высотой H и основаниями S1 и S2, доверху заполнен водой и стоит на весах основанием S1.
Очевидно, что массу воды в сосуде можно вычислить как M=rV, где r – плотность воды. С другой стороны, также очевидно, что вода в сосуде оказывает давление rgH на дно (S1), откуда, используя формулу объема цилиндра, легко получить вторую формулу для массы, но уже зависящую от S1 и S2. Откуда же берется разница в массах?


+ 0 -

Ответ

Решение задачи

Ваши ответы на задачу

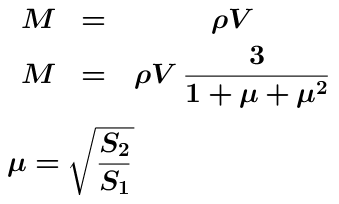
ответов: 11

jonson-72 2018-03-05 14:18:40 пишет:

А вот образец корректного Ответа на Вопрос задачи
"ОТКУДА ЖЕ БЕРЕТСЯ РАЗНИЦА В МАССАХ?":
(оформляю/формулирую обоснование целиком)
p = ρgH ; F = ρgH·S1 ; m = (ρgH·S1)/g = ρ·(H·S1) = ρ·V(ц) ;
• Из формулы Давления мы вывели, что Масса воды давящей на круг S1 равна Массе воды в Объёме ЦИЛИНДРА с основанием S1 (и Высотой уровня воды). – Следовательно "разница в массах берётся" ИЗ РАЗНОСТИ Объёмов _цилиндра_ (с Площадью дна сосуда) и _всего_сосуда_.
• Для усечённого конуса это будет:
V(ук) = H·S1·(1 + sqrt(k) + k)/3 ; (k = S2/S1) ; => ...
Δm = ρ·H·S1·[(1 + sqrt(k) + k)/3 – 1] ; – ...и _совершенно_очевидно_, что эта цифра ТОЖДЕСТВЕННА величине [вертикальной составляющей Давления воды на стенки сосуда].
– – – – – – – – – – – – – – – – – – – – – –
Теперь Вопрос от Решающего Автору: если я УЖЕ имею 100% верную цифру, полученную более простым путём (без вышмата), то какой смысл мне считать ЕЁ ЖЕ путём окольным? – чтобы доказать Автору, что Решающий _тоже_ *грамотный*? – ok :)
– – – – – – – – – – – – – – – – – – – – – –
....Вышматный окольный путь вон озвучил *грамотный* (в отличие от меня) Ар-ту, – интересно, будет ли ему "тырешила"?

jonson-72 2018-03-05 12:56:05 пишет:

да ЗНАЮ, ЗНАЮ :) – сам первый осознал, что это _Я_ накосячил в прошлый заход, – ещё по пути домой понял (имея в голове освежённую визуальную картинку формулы), – но было уже поздно.

....Просто тот пост я писал по памяти, не имея перед глазами картинки с формулами, – ...и выпустил из сознания, что "мю" не все "S" убрал из формулы – одна, вынесенная за скобки, там таки осталась:). .... +Там, где в тот раз заходил в сеть, возможности вдумчиво всё перепроверить "на местности" не было.... – Ну ничего! – тем веселее! (есть тут..."любители попкорна" хрЕновы)
– ивана, если пожелаете, можете тот коммент стереть.

Теперь-то я вижу, что был не прав, и всё там верно (просто "0" исключается из допустимых значений для S1).
• Если принять S1 за константу – как площадь нижнего основания, то тогда всё действительно куда как наглядно.
k (ex-мю) = S2/S1 (лучше оставить так – в сумме будет на одну операцию меньше)
• V = H·S1·(1 + sqrt(k) + k)/3 ;
«V = H·S1» – это Объём "цилиндра-прототипа" ;
«(1 + sqrt(k) + k)/3» – это "коэффициент конусности", – предельные значения: "внутрь" = 1/3 ; "наружу" = ∞.

R-2 2018-03-03 21:11:55 пишет:

Не понимаю в чем проблема. Все работает но нужно упростить задачу, чтобы было меньше формул. Их тяжело описывать словами, а графикой я вообще не могу.
Рассмотрим простой случай. В Ваших терминах: S2 = 0. В моих: конус высоты H, с основанием радиуса R, и образующей L.
Площадь поверхности конуса в развернутом виде - это интеграл по x от нуля до L, от x умножить 2 пи R / L. Т.е. пи * R * L.
Теперь находим интеграл давления по всей площади. Для этого под-интегральное выражение умножаем еще на x * (H/L). Ответ: (2 пи / 3) * R * H * L.
Вертикальная составляющая будет меньше в (R/L) раз. Т.е. (2/3) пи R квадрат * Н. Это и есть (2/3) от объема цилиндра.
Итого, Когда стоит конус, дно давит как цилиндр, а стенки поднимаются вверх с силой в 2/3. Т.е. вся фигня давит как (1/3). А это и есть объем конуса. (1/3) пи R квадрат H.
Все правильно.

R-2 2018-03-01 02:12:53 пишет:

Вопрос в задаче звучит так: "Откуда же берется разница в массах?" Я на него ответил.

ivana2000: Нужно доказать. Это и будет ответом.

R-2 2018-02-28 19:31:47 пишет:

Что я и говорил с самого начала.

jonson-72 2018-02-28 19:23:44 пишет:

> "Соответственно, сила, действующая на чашу весов, равна ρgH·S₁"
== бред:)
1) на чашу весов действует не _ВОДА_, а _СОСУД_(с водой) – жёсткая твёрдая материя – совершенно любой формы. При константной Массе, Вес его тоже константен, – при любой площади основания.
2) вода же действует не только на S₁, но на _ВСЮ_ внутреннюю площадь сосуда, с которой она контачит – _ПО_НОРМАЛИ_ к ней.
3) у вас проблемы с физикой (гидростатикой)? :)

ivana2000 2018-02-28 16:36:18 пишет:

ДД, ρgH к тому, что давление жидкости на дно зависит ТОЛЬКО от глубины дна. Соответственно, сила, действующая на чашу весов, равна ρgH·S₁ и уравновешивается реакцией весов.

Вычислив высоту конуса H через V, S₁ и S₂, получим вторую формулу для массы (или показаний весов), из которой следует, что
если S₁>S₂ (μ<1), то M>ρV,
если S₁<S₂ (μ>1), то M<ρV,
если S₁=S₂ (μ=1), то M=ρV.
Т.е. масса вроде бы зависит от формы.

jonson-72 2018-02-27 15:10:16 пишет:

Первая формула (M=rV) – это такая же физическая Аксиома как и закон Ома. И Всё что к ней приписано/дописано – нелегитимно по определению.

А далее вы просто вычисляете это самое "В" посредством формул геометрии. – К чему там вышеупомянутое "rgH" и в чём конкретно "парадокс" – _вообще_непонятно_ (по Условию, – не по давно известной идее), – задача-то В ЧЁМ? (ещё одна типа "задача"?)

Идея о выведении Силы, давящей на дно через Давление на Площадь (+через "же" Массы) – не нова. Но(!) это будет Масса только [цилиндра] воды с основанием S1, а не конуса (В-писанного в него, или О-писанного – тоже не ясно:).

Ар-Ту всё уже сказал – давление на стенки формульно описывается в разделе Гидростатика, – и _здесь_ оно имеет также и вертикальную составляющую, которой на опору давит вода, не поместившаяся в цилиндр.

R-2 2018-02-24 06:09:27 пишет:

Вы меня не видите? Да, нет?

ivana2000: Пока – нет.

ivana2000 2018-02-24 02:54:31 пишет:

В условиях есть опечатка.
«... используя формулу объема цилиндра ...» следует читать как «... используя формулу объема усеченного конуса...».

R-2 2018-02-20 18:24:25 пишет:

Вода давит не только на дно, но и на стенки сосуда (и поднимает себя за волосы.)

Добавьте комментарий:

Обсуждаем

Задача Разрезанный треугольник:
http://lprobs.ru/img/yes.gif : [скрыто]
Гостевая книга:
не представился : Это было в 1913 году. Одиннадцатилетняя девочка, пансионерка Московской Ржевской гимназии очень прос...
Задача Гора.:
Xuzke : [скрыто]
Гостевая книга:
не представился : В школе все казалось правильным. Из математики следует физика, из физики следует химия, из химии сле...
R-2 : Ты решил: Ну, и наконец, то решение, которое тут видимо предполагается в идеале, я не буду говори...
Так, по старой памяти заглянул :) : R-2, условие неплохо бы конкретизировать. ;)) А то так вариантов может быть масса, хотя все обладают...
Задача 4 хода:
колд : [скрыто]
Задача Кот и мышка:
Дмитрий : [скрыто]
Задача Черная Жемчужина:
mskfirst : [скрыто]
Задача Квадратный торт:
не представился : [скрыто]
Задача Задача с ведрами: 9 и 4 = 6.:
ИносОйЧанбин : [скрыто]
Дкгк7 : [скрыто]
Задача Геометрическая 3:
не представился : [скрыто]
Алексей : [скрыто]
Гостевая книга:
R-2 : Дано: листочек бумаги и ручка. На листочке написаны три нуля. О О О Задача: «как из трёх нулей...

Реклама

© 2009-201x Логические задачи

Задачи на логику и сообразительность

Поиск на сайте

Задачи

Данетки

Справочная

Реклама

задача: Дефект масс

Ответ

Решение задачи

Ваши ответы на задачу

Обсуждаем

Реклама