
О сайте
Гостевая книга
ЧаВо
Пользователи
RSS
|
/в разделах "Логические" "Стратегии" "Чисто поржать"
2017-10-05 /
В социальных сетях стала популярной фотография, которую опубликовал один из пользователей. На снимке изображен кухонный шкаф, с полок которого упала часть тарелок. Если дверцу шкафа открыть - тарелки упадут на пол и разобьются. А как бы Вы выкрутились в этой ситуации? ... решать
|
/в разделах "Логические" "Стратегии"
2017-09-27 /
На столе лежит колода из 52 карт. Алекс, Бен и Карл по очереди берут 1 или 2 карты из колоды. Выигрывает тот, кто взял последнюю карту. Первым ходит Алекс, затем Бен, затем Карл и далее по кругу. Есть ли у кого-либо из игроков стратегия, которая позволит ему выиграть, даже если двое других действуют сообща? ... решать
|
/в разделах "Геометрические" "Стратегии"
2017-06-19 /
У двух игроков есть кубическая картонная коробка, в которой лежит приз. Они по очереди выбирают одно из рёбер коробки и разрезают коробку вдоль этого ребра. Выигрывает тот, после чьего хода можно открыть коробку и достать приз. Есть ли у кого-либо из игроков выигрышная стратегия в такой игре (коробка открывается, если она разрезана вдоль трёх рёбер одной грани)? ... решать
|
/в разделах "Логические" "Стратегии"
2017-06-08 /
На входе в хранилище банка стоит охранник. Рядом притаился шпион. Подходит к охраннику один служащий банка, охранник ему: "Шесть". Служащий в ответ: "Пять". Охранник пропустил. Следующий подходит - охранник: "Пять", служащий: "Четыре". Охранник пропустил. Рискнул шпион, подходит - охранник: "Четыре", шпион: "Три". Охранник с воплями: "Неправильно, попался, гад!" скрутил шпиона. Вопрос: почему неправильно и каков правильный ответ? ... решать
|
/в разделах "Стратегии"
2017-04-11 /
В маленьком гаражном комплексе всего двенадцать помещений, обозначенных буквами, восемь их них заняты автомобилями. Вам нужно передвинуть автомобили под номерами 1, 2, 3 и 4 на места автомобилей 5, 6, 7 и 8. Примечание: выезжать за пределы гаражного комплекса автомобили не могут. ... решать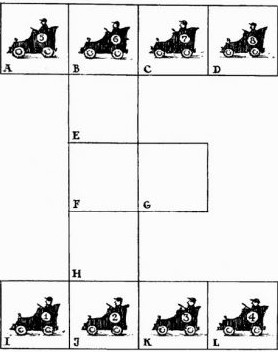
|
/в разделах "Логические" "Стратегии"
2016-12-13 /
Вы дали старому другу новый номер своего сотового, но не уверены, что тот его правильно записал. Так получилось, что вы с ним встретились на конференции, но не можете поговорить: он сидит в президиуме, а вы в зале. Зато можете передать другу любое число записок, но только через помощницу, которая все их читает. Сразу после выступления друг уезжает, и вы не увидитесь лично. Его телефона у вас тоже нет. Как вам проверить, правильный ли номер записал ваш друг, и как, если что, передать ему верный, но так, чтобы помощница не узнала ваш телефон? ... решать
|
/в разделах "Вопросы на эрудицию" "Стратегии"
2016-10-19 /
В некой структуре (не буду её упоминать, чтобы не искушать воспользоваться поиском) новый глава выбирался голосованием. Сначала можно было голосовать за любого члена сообщества. Если не было явного лидера (скажем, набравшего более 50% голосов), то проводился второй тур среди тех, кто набрал большее число голосов. Однажды эти выборы выиграл человек, которого никто не собирался делать главой. Как ему это удалось? ... решать
|
/в разделах "Стратегии"
2016-09-17 /
Четыре пивные кружки расставлены по краям квадратного стола, некоторые вверх ногами. По столу ползает робот исполняющий три команды (а) «перевернуть угловую кружку» (б) «перевернуть две диагональных кружки» (с) «перевернуть две соседние кружки». Однако после каждой команды непредсказуемо в каком углу, на какой диагонали или стороне стола кружки приглянутся роботу больше. Придумайте серию команд понуждающую робота привести кружки хотя бы к единообразию.
Поделился Benjamin Rossman. ... решать
|
/в разделах "Геометрические" "Стратегии"
2016-07-31 /
Лист бумаги разбит регулярной решеткой правильных шестиугольников (соты), некоторые шестиугольники по краям листа будем полагать неправильными, но по меньшей мере один влазит целиком. Вообразите теперь, что шестиугольники беспорядочно раскрашены в черный и белый цвета. Докажите что существует черная тропинка сверху вниз листа, либо белая слева направо. ... решать
|
/в разделах "Логические" "Математические" "Стратегии"
2016-06-13 /
Отец в целях стимуляции сказал сыну, что сколько бы он не заработал, то есть сын, папа даст ему еще квадрат этой суммы. Семья небогатая была. Сын на следующий день заработал 10 $. У отца было в кошельке 500$. Но он не смог дать сыну его заслуженные деньги,так так не хватило. Как же так, почему не хватило? ... решать
|
/в разделах "Стратегии"
2016-06-06 /
Перед детьми 2 кучи орехов. Девочка и мальчик придумали такую игру: каждый из них по очереди одну кучку орехов перекладывает на тарелку, а другую делит на 2 меньшие кучки. Проигрывает тот, кто при своём очередном ходе не сможет разделить кучку, так как в ней остался только один орех. Девочка начинает первой. Как она должна играть, чтобы выиграть, если в начале игры в одной из кучек было 24 ореха, а в другой – 19? ... решать
|
/в разделах "Стратегии"
2016-06-02 /
Имеется ряд из 15-и клеток. На крайней левой клетке - 3 пуговицы. Каждый может перенести любую пуговицу на любое число клеток вправо. Проигрывает тот, кому некуда ходить. У кого есть выигрышная стратегия? ... решать
|
|  | | Задача Разрезанный треугольник:
http://lprobs.ru/img/yes.gif : [скрыто]
Гостевая книга:
не представился : Это было в 1913 году. Одиннадцатилетняя девочка, пансионерка Московской Ржевской гимназии очень прос...
Задача Гора.:
Xuzke : [скрыто]
Гостевая книга:
не представился : В школе все казалось правильным. Из математики следует физика, из физики следует химия, из химии сле...
R-2 : Ты решил:
Ну, и наконец, то решение, которое тут видимо предполагается в идеале, я не буду говори...
Так, по старой памяти заглянул :) : R-2, условие неплохо бы конкретизировать. ;)) А то так вариантов может быть масса, хотя все обладают...
Задача 4 хода:
колд : [скрыто]
Задача Кот и мышка:
Дмитрий : [скрыто]
Задача Черная Жемчужина:
mskfirst : [скрыто]
Задача Квадратный торт:
не представился : [скрыто]
Задача Задача с ведрами: 9 и 4 = 6.:
ИносОйЧанбин : [скрыто]
Дкгк7 : [скрыто]
Задача Геометрическая 3:
не представился : [скрыто]
Алексей : [скрыто]
Гостевая книга:
R-2 : Дано: листочек бумаги и ручка. На листочке написаны три нуля.
О О О
Задача: «как из трёх нулей...
|
|
