Логические задачи : Касательный шар

	"Логические задачи" - это познавательно-развлекательный проект для непрокисших мозгов. Задачи на логику, нестандартное мышление. Не всегда самое очевидное решение - правильное. Но иногда всё оказывается проще, чем кажется на первый взгляд.
Задачи на логику и сообразительность
Главная \| О проекте \| Все задачи-1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C \| Добавить задачу

О сайте
Гостевая книга
ЧаВо

Пользователи
RSS

Поиск на сайте

запомнить меня

Задачи

Переливания и взвешивания

Теорвер, комбинаторика

Задания на наблюдательность

требуется помощь

Чисто поржать

Детские с подковыркой

Данетки

Текущие:

  Мой любимый грех (с)
  Математика в архитектуре
  Не сыпь мне соль на рану
  «Геометрическая»
  Высказывание Ломоносова
  Наверное, не про яблоки
  Комерция
  Везде градусы
  Вагончик тронется, вагончик тронется..
  Спасибо медикам и католикам))
  Специальная купюра
  Студенческая смекалка
  Эллипс vs Круг
  Современные технологии. Немецкий стандарт.
  Спортивная
  философская
  Про газету
  печатная монета
  Купюра евро
  Древние изобретения
  Биометрические паспорта
  Новый глава
  В далеком созвездии тау Кита... 8)))
  Огородное
  Средневековое строительство
  Жестокое наказание
  Их нравы - 4
  Европейский стандарт

Разгаданные недавно:

  этот модный тандыр
  Из Что-Где-Когда
  Может ли такое быть?
  Что изображено?
  Да на тебе пахать надо!

Справочная

Признаки делимости
Площади фигур

Реклама

Версия для смартфонов

задача: Касательный шар

Задачу прислал: ivana2000

В квадрат со стороной 2 вписываются 4 одинаковых круга диаметра 1 (смотрим картинку). В центр вписывается круг, касающийся первых четырех кругов. Аналогичным образом центральный шар вписывается в куб с ребром 2. Операция обобщается на пространство с N измерениями.
Требуется определить к какому числу стремится отношение объема N-шара к объему N-куба при достаточно большом N.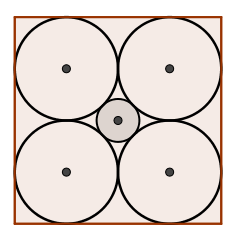


+ 1 -

Ответ

Решение задачи

Ваши ответы на задачу

ответов: 14

ivana2000 2018-05-15 11:13:35 пишет:

«- сперва, с какого-то перепугу...»
KoKos, Вы сами расписались в том, что написали чушь. И скажу Вам по секрету: все задачи и их решения откуда-то списываются.

«- затем вы проделываете кучку...»
Да, это мое право, поэтому Вы опять сморозили чушь.
Кучка преобразований, занимающих ~10 мин., нужна для того, чтобы упростить исходное соотношение и показать что и из чего получается. Разумеется, тем, кому это неинтересно, могут пропустить выкладки.
Интересно, каким из двух замечательных пределов Вы пользовались? А доказать сможете?

«- а в конце Вы просто громоздите...»
Возведение в квадрат удобно для того, чтобы избавиться по возможности от иррациональностей.
Для положительных чисел, если a>=<b, то a²>=<b² и наоборот. Это, наверное, в первом классе проходят. KoKos, включите, наконец, голову.
Объем в геометрическом его понимании не может быть отрицательным, т.к. определяется суммированием положительных величин dV по некоторой области.

«- и вишенка на тортике»
KoKos, теперь я в курсе, что «вишенка» состоит в том, что Вы не умеете читать, т.к. сморозили очередную, причем несусветную, чушь. Прочтите внимательно и посмотрите на график. Вот это действительно УРА!

KoKos 2018-05-15 07:08:24 пишет:

ivana2000, Вы не перестаете меня удивлять. :) Вы хоть читали мое решение - что сделали из него такой вывод? 8)) А тот набор букв, который, по идее, должен свидетельствовать о том, что "Автор пользуется головой", на самом деле говорит прямо противоположное. Судите сами:

- сперва, с какого-то перепугу, ребро куба оказалось уже 4, тогда как в Вашем же собственном условии оно 2. Я понимаю, конечно, что на отношении это никак не сказывается, но создает устойчивое впечатление, что решение списано с другой похожей задачи;
- затем вы проделываете кучку никому не нужных манипуляций с разложением логарифма - Ваше право, конечно, самому себе усложнять жизнь, но воспользоваться замечательным пределом, как это сделал я, было бы куда как легче :)
- а в конце Вы просто громоздите перл на перле. В задаче требуется найти отношение объемов - ЗАЧЕМ Вы возводите его в квадрат??? 8))) То, что его квадрат стремится в бесконечность, отнюдь не означает, что само отношение стремится туда же - не так ли? А вдруг какое-нибудь еще "чудо многомерной геометрии" предполагает существование отрицательных объемов? XD XD XD
- и вишенка на тортике это вывод "A>1 => Aⁿ*B(n) -> ∞" - Вы в курсе, что у Вас второй множитель В(n) при этом стремится к нулю и требует оценки и "четкого математического обоснования"? Или мы теперь будем считать, что например (2/10)ⁿ тоже стремится в бесконечность? Ну а что, разделим на два множителя 2ⁿ*1/10ⁿ, 2>1 ура? XD

ivana2000 2018-05-14 21:58:15 пишет:

А вот график отношения вблизи перехода через единицу. Видно, что при n=1204 объем куба еще превосходит объем шара, а при n=1205 уже нет.

Похоже, KoKos, это именно Вы решили тупо в лоб считать Г-функцию и (√n - 1)ⁿ для больших чисел, строить графики и тупо же смотреть на результат. Не получилось? Облом? Вы бы еще теорвер и статистическую физику перевели бы на схему случаев и вычисляли бы в лоб всякие C(n,m), n!, nⁿ для безумных значений. Ни одна программа не справится. Поэтому-то и были разработаны всевозможные предельные, асимптотические и прочие методы, существенно упрощающие численные расчеты. Но для этого, конечно, нужна голова, которой Автор и пользуется, а график, кстати, без всяких проблем сделанный в Геогебре, – всего лишь иллюстрация решения.

ivana2000 2018-05-14 21:57:45 пишет:

Получаем асимптоту для объема ЦШ, делим её на объем куба, возводим в квадрат и получаем асимптотическую формулу для отношения объемов.
Второе «чудо» состоит в том, что отношение объемов зависит от величины
πe/8 ≈ 1.0675 > 1,
что и приводит к тому, что отношение объемов стремится к бесконечности. Т.о. вписанный в n-куб n-ЦЩ в конце концов превысит не только размеры, но даже и объем куба.
Вот такие вот палочки и транспортиры.

ivana2000 2018-05-14 21:57:06 пишет:

Чтобы найти асимптоту для
(√n - 1)ⁿ
придется воспользоваться разложением ln(1+x) и известной формулой
a^b=e^[ln(a^b)]=e^[b·ln(a)].

ivana2000 2018-05-14 21:56:41 пишет:

Для центрального шара (ЦШ) в кубе с ребром 4 его радиус будет равен
√n - 1.
Это первое «чудо», т.к. радиус ЦШ очень быстро становится и больше ребра куба и больше радиуса угловых шариков, оставаясь тем не менее ими зажатым.
На картинке VS – объем ЦШ, R – радиус ЦШ, VC – объем куба.
Гамма-функция является обобщением факториала натуральных чисел на числа действительные:
Г(x + 1) = xГ(x), в часности
Г(n + 1) = n!
Асимптота для n! легко находится по формуле Стирлинга, а вот с (√n - 1)ⁿ все обстоит гораздо хуже.

KoKos 2018-05-13 18:07:59 пишет:

И в заключение. :) Очень похоже, что кто-то (необязательно именно Автор) при составлении задачи пользовался геогеброй вместо головы. :)) Судя по формулировкам "к числу стремится" и "при достаточно большом", а также по тому факту, что несмотря на обладание рядом достоинств, геогебра неважно справляется с обобщенными гамма-факториалами - обатите внимание на картинке слева, где заканчиваются вычислительные способности программы, если ее в лоб попросить "проанализировать" искомое отношение. :) Недвусмысленно навевает мысли об асимптотическом стремлении... Но если таки просто включить голову, то даже не обладая необходимыми для решения задачи познаниями, можно попросить у той же геогебры более детальный зум - на котором отчетливо видно локальный экстремум где-то в районе 260 измерений и после него явно загибающееся вверх продолжение. :) Ну, а как оно ведет себя дальше, мы уже знаем.

KoKos 2018-05-12 12:28:22 пишет:

Ну и поехали ковыряться. Формула объема гипершара в произвольном N-мерном евклидовом пространстве - это пи^(N/2)/(N/2)!*эр^N . Факториал дробного числа для нечетных эн определяется через эйлеровскую гамма-функцию. Подставляем наше эр=(√N-1)/2, делим на объем гиперкуба 2^N, и разваливаем неудобоваримый факториал по формуле Стирлинга. Получаем все равно довольно неудобоваримую кракозябру, но если в ней немножко поперетасовывать множители с места на место, то получается хоть мало-мальски симпатичная функция h(x), описывающая искомое отношение объемов гипершара и гиперкуба в зависимости от размерности пространства х (см. картинку). Сама по себе эта функция нам тоже на глаз ничего хорошего не говорит, поэтому мы ее еще и прологарифмируем, чтобы понять куда же она ползет при больших иксах. После логарифмирования получим р(х) - ее график и видим на картинке. То бишь, сперва отношение объемов таки падает близко к нулю - так что те, для кого двухсотмерное пространство будет "достаточно большим эн", :))) а е-в-минус-десятой - достаточно малым, могут утверждать нулевое отношение объем с чистой совестью. :))) Однако с дальнейшим увеличением размерности пространства, гипершар все же медленно но верно побеждает гиперкуб, с отношением объемов стремящимся неограниченно в плюс бесконечность.

Небольшое пояснение, почему так. Смотрим там же на картинке на соседнюю функцию р1(х) - это та же р(х) только еще чутка преобразованная. x*ln((√x-1)/√x) заменен своим пределом, который равен -√х просто для большей наглядности. Что мы имеем? Три "рабочих" слагаемых (логарифм корня из пи - константа, и на поведение в бесконечности, соответственно, никак не влияет). Впереди у нас линейный икс с маленьким множителем (половина логарифма пи*е/8 это около трех сотых) - так что поначалу несчастный икс задавленный множителем нервно курит бамбук. Но дальше идут минус корень икса и минус логарифм корня икса - которые никак не могут состязаться с иксом в скорости роста, так что как только мы выбираемся на размерности, исчисляемые тысячами, линейный икс вылазит из-под своего мелкого множителя и спокойно давит конкурентов. Еще там минус единица на шесть икс в хвосте добавилась - чисто для того, чтоб никто не смог подкопаться под допустимость замены факториала по формуле Стирлинга на приближенное значение. :) Этот последний хвостик дает оценку приближенного значения вверх, соответственно, будучи в знаменателе, уменьшает общее отношение - как видим, даже уменьшенное, оно все равно бодро топает в бесконечность.

ivana2000: Похоже.

KoKos 2018-05-12 11:28:54 пишет:

Держите, ivana2000, свое четкое математическое обоснование.

Во-первых, нам достаточно рассмотрение ограничить лишь одним углом гиперкуба (четвертью для нарисованного квадрата и т.д. - см. картинку) Все интересующие нас точки лежат на главной диагонали - центры "подпирающего" и "подпираемого" (искомого) гипершаров (по условию) и, соответственно, точка их касания (всегда лежащая на прямой, соединяющей центры).

Главная диагональ гиперкуба размерности N составляет а√N - по старому доброму Пифагору - и, соответственно, неограниченно растет с ростом размерности пространства - а вместе с ней так же неограниченно растет и радиус подпираемого гипершара. В нашем "уголке" интересующий нас кусок главной диагонали (половина) составит как раз √N ровно. При этом радиус подпираемого гипершара, как легко видеть, составляет половину главной диагонали без диаметра подпирающего гипершара (который по условию постоянен и равен единице) да еще пополам за счет симметрии - итого (√N-1)/2 . Что я и прохлопал с наскоку предположив что подпираемый гипершар всегда будет внутри гиперкуба.

Собственно, на этом "чудные открытия" которые может преподнести данная задачка человеку непосвященному и заканчиваются. :) Дальше требуется определенное количество специальных знаний и куча скушной возни с громоздкими формулами. Продолжение следует отдельным постом.

KoKos 2018-05-11 14:41:23 пишет:

ivana2000, я попрошу Вас *тоже* воздержаться от необоснованного флуда, раз уж Вы его старательно пресекаете в исполнении других - а то как-то очень неравные условия у нас получаются, не находите? :)) В данном случае Ваша субъективная оценка моих личных качеств, не имеющая ничего общего ни с задачей, ни с реальностью, именно таковым и является. :)

ivana2000 2018-05-11 11:54:54 пишет:

Забавно то, KoKos, что Вы сходу не решили задачку каким-нибудь лайфхаком, хотя Вас уже понесло в этом направлении.

Для тех, кто не в теме, советую почитать KoKosовские комментарии к задаче «Полезное неравенство», где он «гениально» переносит свойства 3-пространства на любое пространство N измерений с помощью трехмерных «палочек» и трехмерных «транспортиров». Кстати, само неравенство имеет опосредованное отношение к N-пространствам, хотя и лежит в основе их теории.

В связи с этим предвижу огромное количество флуда без малейших элементарных обоснований от человека, считающего себя «знатоком» N-мерных пространств, но не знающего элементарные основы многомерной геометрии.

KoKos, слова не нужны, нужно
ЧЕТКОЕ МАТЕМАТИЧЕСКОЕ ОБОСНОВАНИЕ.

KoKos 2018-05-11 01:25:04 пишет:

И да, в 9-тимерном, конечно же, догонит, а не в 25-тимерном.

KoKos 2018-05-11 01:18:02 пишет:

Хотя нет, это я поторопился. Уже в 25-тимерном пространстве искомый гипершар догонит и сольётся в экстазе с вписанным единичным гипершаром, а с дальнейшим увеличением размерности пространства начнёт его обгонять и выпирать за пределы исходного гиперкуба. Тогда сложность явно занижена. 8)

KoKos 2018-05-11 00:50:38 пишет:

Забавно… ivana2000, каким ветром Вас занесло в многомерную-то? 8)

Задача гораздо проще, чем может показаться на первый взгляд. Стараться и расписывать объём дофигамерного гипершара и пытаться сравнивать его с объемом соответствующего гиперкуба вовсе не нужно, как не нужно и знать подробностей гамма-функции, и т.п. :) Достаточно вписать в наш квадрат-куб-…-гиперкуб другой круг-шар-…-гипершар - единичного *радиуса*. Этот новый гипершар будет очевидно больше искомого, а вот его объём, как широко известно, стремится к нулю при достаточно большом эн, причём довольно резво. :))) Соответственно, ровно к тому же нулю будет стремиться и объём меньшего искомого гипершара - деваться-то ему некуда. А объём гиперкуба, напротив, будет радостно ползти в плюс-бесконечность, как два в степени эн. Так что их отношение будет все тот же ноль, стремительным домкратом. :)

Добавьте комментарий:

Обсуждаем

Задача Гора.:
Xuzke : [скрыто]
Гостевая книга:
не представился : В школе все казалось правильным. Из математики следует физика, из физики следует химия, из химии сле...
R-2 : Ты решил: Ну, и наконец, то решение, которое тут видимо предполагается в идеале, я не буду говори...
Так, по старой памяти заглянул :) : R-2, условие неплохо бы конкретизировать. ;)) А то так вариантов может быть масса, хотя все обладают...
Задача 4 хода:
колд : [скрыто]
Задача Кот и мышка:
Дмитрий : [скрыто]
Задача Черная Жемчужина:
mskfirst : [скрыто]
Задача Квадратный торт:
не представился : [скрыто]
Задача Задача с ведрами: 9 и 4 = 6.:
ИносОйЧанбин : [скрыто]
Дкгк7 : [скрыто]
Задача Геометрическая 3:
не представился : [скрыто]
Алексей : [скрыто]
Гостевая книга:
R-2 : Дано: листочек бумаги и ручка. На листочке написаны три нуля. О О О Задача: «как из трёх нулей...
Задача Мышки и бутылки:
Никита : [скрыто]
Задача Вписанные квадратики:
Маргарита : [скрыто]

Реклама

© 2009-201x Логические задачи

Задачи на логику и сообразительность

Поиск на сайте

Задачи

Данетки

Справочная

Реклама

задача: Касательный шар

Ответ

Решение задачи

Ваши ответы на задачу

Обсуждаем

Реклама