
О сайте
Гостевая книга
ЧаВо
Пользователи
RSS
| задача: Кинематика циркулем и линейкой |
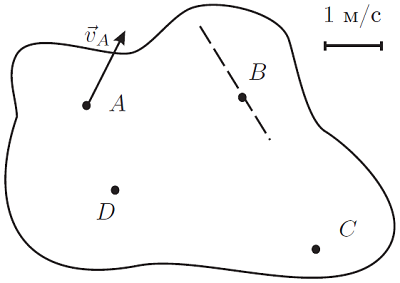
 Плоское тело движется по плоскому столу. В некоторый момент времени точка A имеет скорость, показанную на картинке. Плоское тело движется по плоскому столу. В некоторый момент времени точка A имеет скорость, показанную на картинке.
1. Постройте скорость точки C, если скорость точки B направлена вдоль пунктирной прямой.
2. Постройте скорость точки C, если модуль скорости точки B равен 1.0 м/c.
3. Постройте скорость точки D, если скорости точек B и C одинаковы по модулю.
ответов: 11
|  | | Гостевая книга:
не представился : Это было в 1913 году. Одиннадцатилетняя девочка, пансионерка Московской Ржевской гимназии очень прос...
Задача Гора.:
Xuzke : [скрыто]
Гостевая книга:
не представился : В школе все казалось правильным. Из математики следует физика, из физики следует химия, из химии сле...
R-2 : Ты решил:
Ну, и наконец, то решение, которое тут видимо предполагается в идеале, я не буду говори...
Так, по старой памяти заглянул :) : R-2, условие неплохо бы конкретизировать. ;)) А то так вариантов может быть масса, хотя все обладают...
Задача 4 хода:
колд : [скрыто]
Задача Кот и мышка:
Дмитрий : [скрыто]
Задача Черная Жемчужина:
mskfirst : [скрыто]
Задача Квадратный торт:
не представился : [скрыто]
Задача Задача с ведрами: 9 и 4 = 6.:
ИносОйЧанбин : [скрыто]
Дкгк7 : [скрыто]
Задача Геометрическая 3:
не представился : [скрыто]
Алексей : [скрыто]
Гостевая книга:
R-2 : Дано: листочек бумаги и ручка. На листочке написаны три нуля.
О О О
Задача: «как из трёх нулей...
Задача Мышки и бутылки:
Никита : [скрыто]
|
|

 Плоское тело движется по плоскому столу. В некоторый момент времени точка A имеет скорость, показанную на картинке.
Плоское тело движется по плоскому столу. В некоторый момент времени точка A имеет скорость, показанную на картинке.